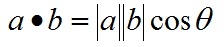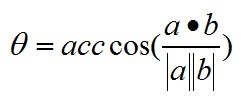游戏开发向量基础

本文讲述游戏开发涉及到的向量基础知识。向量是游戏开发中的基础，本文总结下向量在游戏开发中常用的基础知识。

1. 点乘

向量的点乘,别名: 点积、内积、数量积。

1.1 代数定义

对两个向量执行点乘运算，就是对这两个向量对应位一一相乘之后求和的操作，点乘的结果是一个标量。

1.2 几何定义

是向量a在向量b方向上的投影与向量b的模的乘积。

用来表征或计算两个向量之间的夹角，以及在b向量在a向量方向上的投影。
a和b间的夹角θ的计算公式为:

可知:

• a·b>0
  方向基本相同，夹角在0°到90°之间
• a·b=0 正交，相互垂直
• a·b<0
  方向基本相反，夹角在90°到180°之间

如上结论需要依赖sin和cos的正负知识点:

• sin：一二象限正，三四象限负。
• cos：一四象限正，二三象限负。

2. 叉乘

别名: 叉积、外积、向量积。
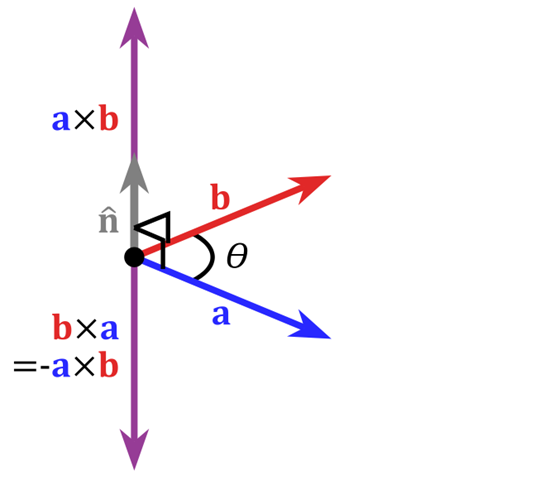
公式: a×b=c，其中|c|=|a||b|·sinθ，c的方向遵守右手定则。
叉乘的运算结果是一个向量而非标量。
两个向量的叉积与这两个向量组成的坐标平面垂直。

2.1 几何意义

三维几何中，向量a和向量b的叉乘结果是一个向量，更为熟知的叫法是法向量。
该向量的方向垂直于a和b向量构成的平面。
模的大小等于由向量a和向量b构成的平行四边形的面积。

3. 直角三角形相关公式

• 正弦函数sinA
  表示在一个直角三角形中，∠A（非直角）的对边与三角形的斜边的比
• 余弦函数cosA
  表示在一个直角三角形中，∠A（非直角）的邻边与三角形的斜边的比